Спеціальний фінансовий блог щодо розрахунку привабливості інвестиційного проекту, який підготував учасник 6 групи програми MSc in Innovations and Entrepreneurship Олег Чагарин. Не лякайтеся цих таблиць – це так надихають наших інноваторів курси «Основи фінансової звітності та фінансового обліку, зокрема їх викладачі.
Ділимося матеріалом Олега Чагарина з вами: «При розрахунку правабливості інвестиційного проекту ми, зазвичай, розраховуємо NPV(Net Present Value) та IRR(Internal Rate of Return) як основні критерії для інвестування. І якщо результат розрахунку NPV при заданих Cash Flow та wacc – це завжди одне число, то з IRR ситуація трохи інша.
Наведемо приклад. Нехай ми маємо такі значення CF:
 При wacc = 25% маємо значення NPV 57.92.
При wacc = 25% маємо значення NPV 57.92.
А тепер порахуємо значення IRR в MS Excel:
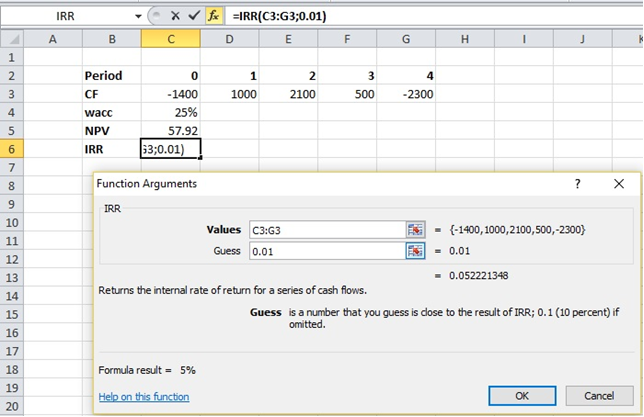
Тут цікавим є поле «Guess» – MS Excel пропонує «вгадати» значення IRR. І справді, якщо ми вводимо значення 1%, Excel повертає значення IRR 5.2%. Якщо ж ми припускаємо, що значення IRR більше – побачимо результат IRR=35.6%:
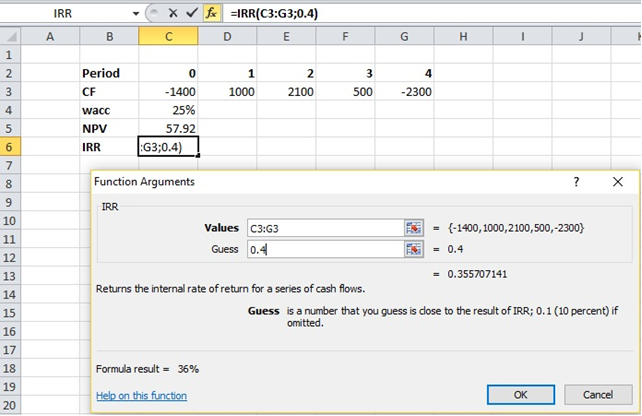
Тобто, для цих значень Cash Flow є, як мінімум, 2 значення IRR і вони обидва правильні. Інтуїтивно це складно собі уявити, оскільки визаченням IRR є «така ставка дисконтування(wacc), при якій NPV дорівнює нулю». Як наслідок, ми є впевнені, що IRR може мати лише одне значення. Як бачимо, це не так, хоча заради справедливості варто зазначити, що для простих проектів (зокрема тих, що мають від’ємний CF в нульовому періоді та позитивний в наступні) IRR має дісно одне значення.
Розберемося, чому це так:
Знайти IRR означає розв’язати таке рівняння відностно r:
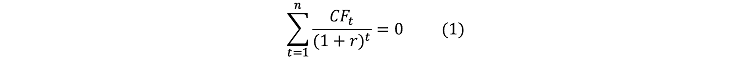
Представимо рівняння (1) в іншому вигляді:
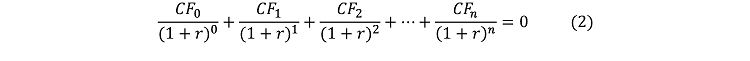
Перемножимо рівняння (2) на :
![]()
У такому вигляді легко побачити, що ліва частина рівняння є многочленом n-го степеня. А з основної теореми алгебри випливає, що многочлен n-го степеня має n комплексних коренів. У випадку IRR нас цікавлять лише дійсні додатні корені. Добре, а скільки таких коренів може бути? І як побачити їх всіх? Для цього нам буде замало інструментарію, який пропонує MS Excel і ми попрацюємо в Matlab. Функція irr в Matlab, застосована до CF, повертає одне значення, якщо є тільки одне значення, яке задовольняє умову, наведену вище і показує попередження, якщо значень кілька: Warning: Multipleratesofreturn.
Запишемо код, який дозволяє знайти усі дійсні додатні значення IRR для заданого CF:

Результат виконання коду:
i2 =
-1.8468 – 0.6592i
-1.8468 + 0.6592i
0.0522 + 0.0000i
0.3557 + 0.0000i
I =
0.0522
0.3557
Маємо такий же результат, як і в MS Excel з той перевагою, що не потрібно вручну «вгадувати» значення IRR.
Задля цікавості спробуємо знайти такі значення грошового потоку, де кількість дійсних додатніх значень IRR становила б принаймні 4 і вони були б менші за 100%.
Запишемо такий код:
 Отримуємо такий результат(це зайняло тривалий час):
Отримуємо такий результат(це зайняло тривалий час):
I =
0.0087
0.3091
0.6426
0.8458
Побудуємо графік значень CF:
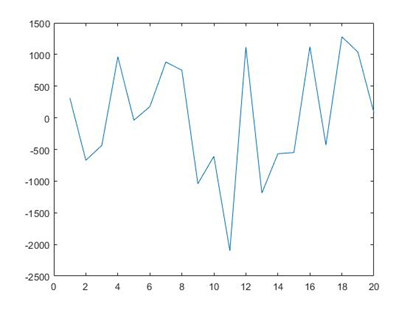
Зрозуміло, що це значення CF, знайдені завдяки симуляції, але вони нас цікавлять лише в ознайомчих цілях.
Побудуємо графік залежності NPV від r для заданих значень Cash Flow:
 Результат:
Результат:
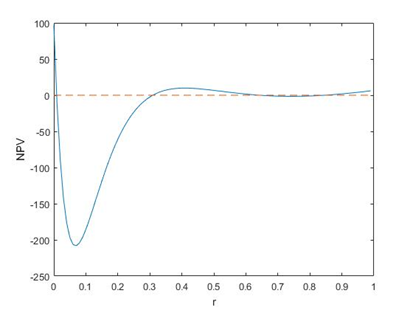
Окей, а що у такому випадку робити? Одна справа – симуляція, а інша – реальний проект. Яке значення IRR брати до уваги, якщо їх кілька? Для цього було придумано показник MIRR(Modified IRR), який вирішує також іншу проблему IRR, а саме, припущення про те, що кошти залучаються та рефінансуються за однаковою ставкою.
Він розраховується за такою формулою:

Як бачимо, ця формула сумує окремо PV від’ємних грошових потоків та FV додатніх грошових потоків і робить це за двома різними ставками. Застосуємо формулу =mirr в MS Excel з припущенням, що ці ставки однакові:
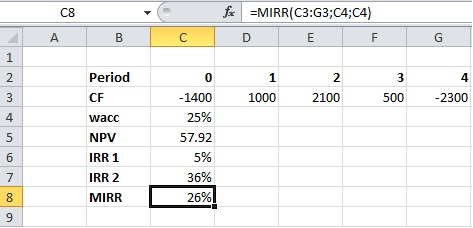
Результат відрізняється від отриманого за допомогою формули irr, проте його очевидна перевага в тому, що значення MIRR можливе лише одне. І на завершення нагадаємо одну важливу річ – порівнювати за допомогою IRR та MIRR варто лише проекти, які потребують однакового розміру інвестицій».






















